在玩折纸中学会几何

一、折纸与几何入门

　　在你手头既没有圆规和刻度尺，又没有三角板和量角器等度量工具和作图工具的情况下，你能准确地比较两条线段的大小吗？能平分一个角吗？能检查两条相交直线垂直与否吗？……

　　比较两条线段的大小，初一几何课本告诉我们有两种基本方法：一种是借助圆规进行图形的叠合，另一种是用刻度尺度量，比较数量的大小．其实，聪明人没有这些工具，也照样能解决这些问题．不是吗？当你还在幼儿园玩拆纸游戏时，就已经在探求解决这些问题的方法了．比如要折“猴婆婆”，老师指导你把一张长方形纸裁成一张正方形纸时，如图1，把长方形纸ABCD的AB边绕点A折叠到AD边上，然后再折叠BE，裁去多余的长方形BECD后，展开即为正方形纸．这样折纸，不正是比较线段大小的最好办法吗？我们把长方形纸的边分别看作线段，这时线段AB与AD的一个端点A重合，另一个端点B落在AD上，因此可知A(B)=AB，AD＞AB；∠(B)AE与∠BAE重合，即AE平分∠BA(B)；∠A(B)E与∠ABE重合，即∠ABE=∠A(B)E=90°，所以纸片A(B)EB是正方形．又如图2，把一张纸任意折叠一次后，再把折痕AB对折(即平分平角)，这时两次折叠的折痕所成的∠COB为直角，利用它就可检查两条相交直线垂直与否，或检查一个角是锐角还是直角或钝角，或检查两个角互余、互补与否．

　　初一几何课本第1页给出了一个五角星，我们可不用任何画图工具，只要一张纸(红纸更好)和一把剪刀，运用折纸办法，就能剪出一个漂亮的五角星，办法如下：取一张纸，先对折成如图3的A(B) EF，再沿OC将BE边折起，得∠BOC，大约使∠BOC=2∠AOB，然后将OC翻折到OB上(折痕OD是∠BOC平分线)，再把∠AOB沿OB叠合到∠DOB上，如图 4；在OA上取一点M，在OB上取一点G，且使OG约等于QM的 2．6倍，最后沿MG直线将折叠成图4状的纸剪开，把剪得的△OMG展开，即成图5那样的五角星．只要经过几次尝试，你一定能熟练地剪出一个漂亮的五角星来．

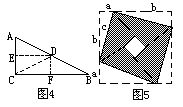
 　　剪五角星的实质是运用折纸五等分平角，同时应用轴对称原理，使如图5中的∠FOA=∠AOK=∠KOE=∠EOP=∠POD=36°，达到∠AOB=∠BOC=∠COD=∠DOE=∠EOA= 72°的目的．

　　你若善于观察思考，将会发现，在儿时玩过的各种折纸游戏中，无不包含最基本的几何原理．反之，学习了几何知识，将会激发你设计创造出更多更新颖的折纸游戏．

　　二、折纸与定理证明

　　折纸既是一种有趣的游戏，更是一种探求几何图形性质的重要方法，特别对于三角形边角关系一类性质的证明，用这种方法真是妙不可言！

　　1．等腰三角形性质的证明

　　取一张等腰三角形纸片，如图1，把两腰AB、AC 折叠在一起．则∠B、∠C重合，即“等腰三角形的底角相等”；折痕AD分别把顶角A、平角BDC、底边BC分成相等的两部分．即折痕AD既是等腰三角形顶角平分线，又是底边上的高和中线．于是得等腰三角形“三线合一”的性质，并且折痕正是证明上述性质时所要添画的辅助线；若在折痕AD上取一点P，连结PB、PC，由于等腰三角形ABC沿AD折叠时，点B与点C重合，所以必有PB与PC重合，于是有“等腰三角形顶角平分线上的点到底边两端点的距离相等”的性质．类似地，可得等腰三角形两腰上的中线相等、底角平分线相等等一系列性质．

　　2．“大角对大边”、“大边对大角”的证明

 　　如图2，取一张纸片△ABC(设AB＞AC)，把AC折叠在AB上，则∠C叠合到了∠AED的位置，有折痕AD、ED，由于∠AED是△BED的外角，故有∠AED＞∠B，即∠C＞∠B，于是有定理“一个三角形中，大边对大角”，并且折痕AD、ED正是证明该定理时所要添画的辅助线．

　　如图3，纸片△ABC，设∠C＞∠B，折叠纸片，使点B与点C重合，则∠B叠合到∠ECD的位置，有折痕ED、EC，可知EC=EB．在△AEC中，AE+ EC＞AC，即AE+EB=AB＞AC，故有定理“一个三角形中，大角对大边”．

　　3．直角三角形性质的证明

　　如图4，取一张直角三角形纸片，设∠C=90°．折叠纸片，分别使点A与点C重合，点B与点C重合，有折痕ED、FD、DC，易知∠A+∠B=90°，中，斜边上的中线等于斜边的一半”．

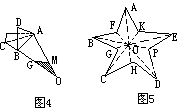
　　如图5，取边长为(a+b)的正方形纸片，将它的四个直角向形内折直角边长为a、=a2+b2，即“直角三角形中，斜边的平方等于两条直角边的平方和”，这是勾股定理的最简证明．